En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo1 de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra 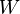 (del inglésWork) y se expresa en unidades de energía, esto es en julios o joules (J) en elSistema Internacional de Unidades.
(del inglésWork) y se expresa en unidades de energía, esto es en julios o joules (J) en elSistema Internacional de Unidades.
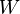 (del inglésWork) y se expresa en unidades de energía, esto es en julios o joules (J) en elSistema Internacional de Unidades.
(del inglésWork) y se expresa en unidades de energía, esto es en julios o joules (J) en elSistema Internacional de Unidades.
Ya que por definición el trabajo es un tránsito de energía,2 nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.
Consideremos una partícula  sobre la que actúa una fuerza
sobre la que actúa una fuerza  , función de la posición de la partícula en el espacio, esto es
, función de la posición de la partícula en el espacio, esto es  y sea
y sea  un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo
un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo  . Llamamos trabajo elemental,
. Llamamos trabajo elemental,  , de la fuerza
, de la fuerza  durante el desplazamiento elemental
durante el desplazamiento elemental  al producto escalar
al producto escalar  ; esto es,
; esto es,
 sobre la que actúa una fuerza
sobre la que actúa una fuerza  , función de la posición de la partícula en el espacio, esto es
, función de la posición de la partícula en el espacio, esto es  y sea
y sea  un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo
un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo  . Llamamos trabajo elemental,
. Llamamos trabajo elemental,  , de la fuerza
, de la fuerza  durante el desplazamiento elemental
durante el desplazamiento elemental  al producto escalar
al producto escalar  ; esto es,
; esto es,
Si representamos por  la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es
la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es  , entonces el vector tangente a la trayectoria viene dado por
, entonces el vector tangente a la trayectoria viene dado por 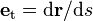 y podemos escribir la expresión anterior en la forma
y podemos escribir la expresión anterior en la forma
 la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es
la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es  , entonces el vector tangente a la trayectoria viene dado por
, entonces el vector tangente a la trayectoria viene dado por 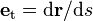 y podemos escribir la expresión anterior en la forma
y podemos escribir la expresión anterior en la forma
donde  representa el ángulo determinado por los vectores
representa el ángulo determinado por los vectores 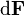 y
y  y
y 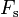 es la componente de la fuerza F en la dirección del desplazamiento elemental
es la componente de la fuerza F en la dirección del desplazamiento elemental  .
.
 representa el ángulo determinado por los vectores
representa el ángulo determinado por los vectores 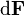 y
y  y
y 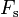 es la componente de la fuerza F en la dirección del desplazamiento elemental
es la componente de la fuerza F en la dirección del desplazamiento elemental  .
.El trabajo realizado por la fuerza
 durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo
durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo  sea agudo, recto u obtuso.
sea agudo, recto u obtuso.
Si la partícula P recorre una cierta trayectoria en el espacio, su desplazamiento total entre dos posiciones A y B puede considerarse como el resultado de sumar infinitos desplazamientos elementales  y el trabajo total realizado por la fuerza
y el trabajo total realizado por la fuerza  en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
 y el trabajo total realizado por la fuerza
y el trabajo total realizado por la fuerza  en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
Esto es, el trabajo viene dado por la integral curvilínea de  a lo largo de la curva
a lo largo de la curva  que une los dos puntos; en otras palabras, por lacirculación de
que une los dos puntos; en otras palabras, por lacirculación de  sobre la curva
sobre la curva  entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza
entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza  sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
 a lo largo de la curva
a lo largo de la curva  que une los dos puntos; en otras palabras, por lacirculación de
que une los dos puntos; en otras palabras, por lacirculación de  sobre la curva
sobre la curva  entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza
entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza  sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.Concepto de energía
Supongamos que F es la resultante de las fuerzas que actúan sobre una partícula de masa m. El trabajo de dicha fuerza es igual a la diferencia entre el valor final y el valor inicial de la energía cinética de la partícula.

En la primera línea hemos aplicado la segunda ley de Newton; la componente tangencial de la fuerza es igual a la masa por la aceleración tangencial.
En la segunda línea, la aceleración tangencial at es igual a la derivada del módulo de la velocidad, y el cociente entre el desplazamiento ds y el tiempo dt que tarda en desplazarse es igual a la velocidad v del móvil.
Se define energía cinética como la expresión

El teorema del trabajo-energía indica que el trabajo de la resultante de las fuerzas que actúa sobre una partícula modifica su energía cinética.
En la primera línea hemos aplicado la segunda ley de Newton; la componente tangencial de la fuerza es igual a la masa por la aceleración tangencial.
En la segunda línea, la aceleración tangencial at es igual a la derivada del módulo de la velocidad, y el cociente entre el desplazamiento ds y el tiempo dt que tarda en desplazarse es igual a la velocidad v del móvil.
Se define energía cinética como la expresión
El teorema del trabajo-energía indica que el trabajo de la resultante de las fuerzas que actúa sobre una partícula modifica su energía cinética.
Ejemplo: Hallar la velocidad con la que sale una bala después de atravesar una tabla de 7 cm de espesor y que opone una resistencia constante de F=1800 N. La velocidad inicial de la bala es de 450 m/s y su masa es de 15 g.
El trabajo realizado por la fuerza F es -1800·0.07=-126 J
La velocidad final v es
|
ENERGIA CINÉTICA
Cuando un cuerpo está en movimiento posee energía cinética ya que al chocar contra otro puede moverlo y, por lo tanto, producir un trabajo.
Para que un cuerpo adquiera energía cinética o de movimiento; es decir, para ponerlo en movimiento, es necesario aplicarle una fuerza. Cuanto mayor sea el tiempo que esté actuando dicha fuerza, mayor será la velocidad del cuerpo y, por lo tanto, su energía cinética será también mayor.
Otro factor que influye en la energía cinética es la masa del cuerpo.
Por ejemplo, si una bolita de vidrio de 5 gramos de masa avanza hacia nosotros a una velocidad de 2 km / h no se hará ningún esfuerzo por esquivarla. Sin embargo, si con esa misma velocidad avanza hacia nosotros un camión, no se podrá evitar la colisión.
La fórmula que representa la Energía Cinética es la siguiente:
E c = 1 / 2 • m • v 2
|
E c = Energía cinética
m = masa
v = velocidad
Cuando un cuerpo de masa m se mueve con una velocidad v posee una energía cinética que está dada por la fórmula escrita más arriba.
En esta ecuación, debe haber concordancia entre las unidades empleadas. Todas ellas deben pertenecer al mismo sistema. En el Sistema Internacional (SI), la masa m se mide en kilogramo (kg) y la velocidad v en metros partido por segundo ( m / s), con lo cual la energía cinética res
Para obtener el valor de la energía potencial elástica podemos razonar de la siguiente manera.
- Vamos a comprimir o estirar un muelle desde su posición de equilibrio (x1 = 0) a posición una posición x2 = x. Consideraremos que el muelle no tiene energía inicial (E1 = 0) por encontrarse en su posición de equilibrio
- Para comprimir o estirar el muelle hemos de ejercer una fuerza igual en magnitud pero de sentido contrario a la ley de Hooke.
F⃗ =k⋅x⃗ - La fuerza ejercida es variable, siendo prácticamente nula al principio y aumentando a medida que aumenta x
- Para calcular el trabajo ejercido por nosotros sobre el muelle, calculamos el área del triángulo limitado por la curva.
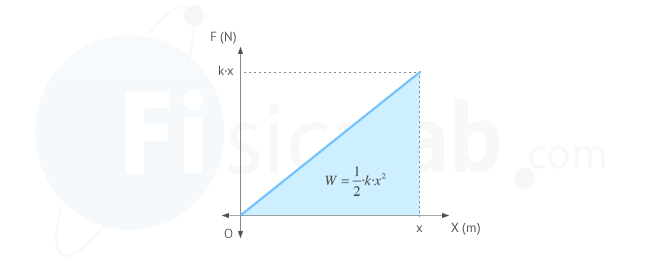
- El muelle, sobre el que hemos realizado el trabajo, ha adquirido energía. Considerando que el trabajo que realiza una fuerza sobre un cuerpo es igual a su variación de energía y que el cuerpo al encontrarse en la posición de equilibrio x = 0 no tenía energía, nos queda que de modo que
Trabajo Realizado por la Fuerza Elástica
Podemos hallar el trabajo realizado por la fuerza elástica o restauradora a través de su relación con la energía potencial elástica.
El trabajo realizado por las fuerzas elásticas es igual a la variación negativa de la energía potencial
¿Cómo se obtiene el trabajo realizado por la fuerza elástica?
Si queremos calcular el trabajo realizado por la fuerza elástica sobre un muelle comprimido que se encuentra en una posición xi y se desplaza a una posición xf , ambas a la izquierda del punto de equilibrio x0, podemos ayudarnos de la siguiente figura y los siguientes razonamientos:
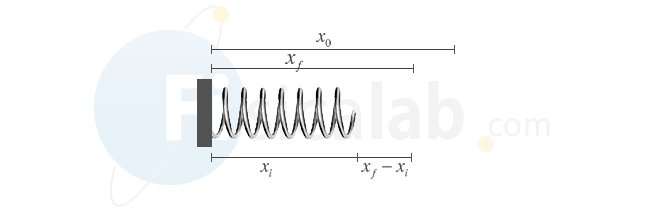
- Será la fuerza elástica la que realizará el trabajo sobre el muelle tratando de llevarlo a su posición de equilibrio.
- La fuerza de recuperación elástica que actúa sobre el cuerpo sigue la ley de Hooke.
F⃗ =−k⋅(x−x0)⋅j⃗ . - Podemos calcular la fuerza en la posición inicial xi según la siguiente expresión
F⃗ i=−k⋅(xi−x0)⋅j⃗ . Observa como, al ser xi < x0, la fuerza apunta hacia la derecha. - Podemos calcular la fuerza en la posición final xf según la siguiente expresión
F⃗ f=−k⋅(xf−x0)⋅j⃗ . Observa como, al ser xf < x0, la fuerza apunta hacia la derecha. - Nos resta el cálculo del trabajo realizado por la fuerza elástica (variable). Tenemos varias opciones:
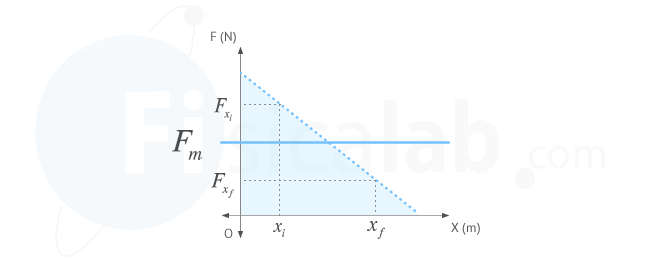
- Podemos calcular el área bajo la fuerza elástica en la gráfica fuerza - desplazamiento. Este procedimiento ya lo hemos señalado en el punto anterior
- Podemos seguir un razonamiento similar al aplicado en el teorema de Merton para el cálculo de la velocidad media: Calcular la fuerza elástica promedio y usar este valor para el cálculo del trabajo. El valor del trabajo de la fuerza elástica (variable) tendrá igual valor que el que lleve a cabo esta fuerza constante de valor promedio.


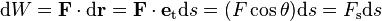
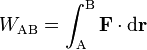
No hay comentarios:
Publicar un comentario